---

アルゴリズムの性能評価方法：primal integralについて

目次

先週の研究室ミーティングで，「Primal Integral（主積分）」という手法を知ったのでメモ．

アルゴリズムの性能評価方法として，これまで自分は「ある時点での目的関数値を比較」するようなことをよくやっていた．

例えば，最小化問題に対するアルゴリズムの評価として，アルゴリズムAは1800secでobj=100，アルゴリズムBは1800secでobj=120が得られたとする．

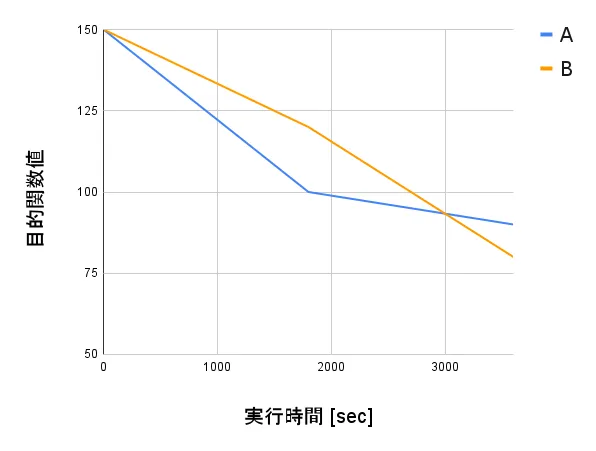
この時，1800secをタイムアウトとすると，アルゴリズムAの方が優れている．といった感じで評価できる．

しかし，タイムアウトを3000secにすると同点，3600secにするとアルゴリズムBの方が優れた解を見つけている． このように，タイムアウトの設定によって，評価が大きく変わってしまう．

ここで，特に実用では，早い段階で良い解を得たいということが多い． 最適化に興味がない人にとっては，それなりの時間でそれなりの解が欲しいということらしい．

このように，「より早く，良い解を」見つけられているかを評価する際にPrimal Integralを使うと良い．Primal Integralはその名の通り，目的関数$f$と横軸$t$で囲まれた部分を$t=1...T$まで積分した値によって評価する． 積分した値が小さいほど，そのアルゴリズムは「より早く，良い解を」見つけたことになる．

参考文献

https://www.msiism.jp/article/solver-performance-evaluation.html